Hattest du schon einmal das Gefühl, dass du in Sachen Beliebtheit im Vergleich zu deinen Freunden am unteren Ende der Fahnenstange bist? Du liegst womöglich richtig. Zumindest eine mathematische Erklärung scheint es für dieses Phänomen zu geben.
Beliebtheit erklärt durchs Inspektionsparadoxon
Das Inspektionsparadoxon kombiniert die doch sehr anti-intuitive Mathematik der Wahrscheinlichkeiten mit der echten Welt. Es verrät, wieso du das Gefühl hast stets besonders lange auf den Bus zu warten oder wieso du denkst, dass deinen Freunden mehr Beliebtheit zusteht als dir.
Für das Bushaltestellen-Beispiel stelle dir bitte einmal folgendes vor: Der Bus kommt laut Fahrplan alle 10 Minuten. Natürlich kommt es mal zu Verspätung oder überraschenden verfrühten Ankünften – schließlich lässt der Verkehr einen gewissen Spielraum.
Nun kommt es jedoch zu einer spürbaren Verspätung von sieben Minuten bei Bus A. Der darauffolgende Bus B ist pünktlich, sodass er drei Minuten als Bus A später kommt. Je nach dem, wie man es rechnet, trifft die Aussage, „der Bus kommt [im Schnitt] alle 10 Minuten“ weiterhin zu. Schließlich sind binnen 20 Minuten zwei Busse (A, B) gekommen. Im Schnitt sind das 10 Minuten Wartezeit pro Bus.
Stets am unteren Ende der Fahnenstange
Doch sollst du jetzt genau in dem Zeitraum, wo Bus A und Bus B eintreffen, eine Inspektion dieser Wahrscheinlichkeit durchführen, wirst du ein anderes Erleben haben. Mit größerer Wahrscheinlichkeit wartest du nämlich länger – und zwar auf Bus A. Schließlich beträgt hier – wegen der Verspätung von sieben Minuten – die durchschnittliche Wartezeit (7 Minuten Verspätung + 10 Minuten planmäßige Wartezeit geteilt durch 2) 8,5 Minuten. Hingegen muss man für Bus B im Schnitt nur 1,5 Minuten warten.
Doch es ist eben realistischer, dass du genau diesen Zeitraum erwischst, wo du länger als im Schnitt wartest. Schließlich ist die Zeitspanne dafür größer. Letztendlich hast du also nicht nur wegen der Verspätung im Vergleich zu Bus B anstelle von durchschnittlich 1,5 Minuten ganze 8,5 Minuten gewartet. Zusätzlich wartest du auch länger als bei planmäßigen Abfahrszeiten, da hier die durchschnittliche Wartezeit fünf Minuten beträgt.
Beliebtheit im sozialen Netzwerk
Aber wieso genau sorgt dieser Umstand jetzt auch noch dafür, dass du über geringere Beliebtheit verfügst als deine Freunde? Das Inspektionsparadox lässt sich auch auf soziale Netzwerke (in der echten sowie der digitalen Welt) übertragen, zeigt Scientific American. Bereits das Bus-Beispiel demonstrierte, dass die Wahrscheinlichkeiten vom Standpunkt (oder Zeitpunkt) der Inspektion abhängen können. Dasselbe gilt auch für deine Freunde.
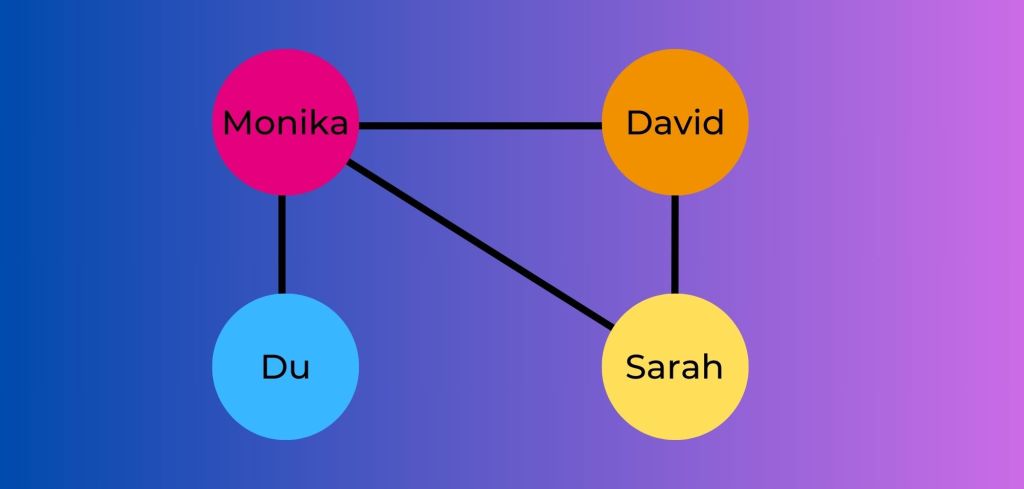
In dem Schaubild, siehst du vier Personen, dich eingeschlossen, als soziales Netzwerk:
- Monika ist mit Sarah, David und dir befreundet, hat also drei Freunde
- David ist mit Sarah und Monika bekannt, hat also zwei Freunde
- Sarah kennt Monika und David gut, hat also zwei Freunde
- Du hingegen bist nur mit Monika wirklich befreundet, hast als eine Freundin
Insgesamt entstehen in diesem sozialen Netzwerk also acht Freundschaften. Erhebt man hieraus den Durchschnitt, hat also jede Person zwei Freunde. Doch die Inspektion zeigt ein anderes Bild über die Beliebtheit der dargestellten Personen. Tatsächlich haben Davids Freunde im Durchschnitt mehr Freunde als du. Du hast schließlich nur eine Freundin und Sarah und Monika haben im Schnitt 2,5 Freunde (Monikas Freunde (3) plus Sarahs Freunde (2) geteilt durch zwei).
Kann es noch schlimmer werden? Diese Studie verrät, dass dich nur die Hälfte deiner Freunde mögen.
Alles eine Sache der Perspektive
Du hast also 1,5 Freunde weniger als andere in diesem Netzwerk und bist damit in puncto Beliebtheit ganz unten. Auch spannend ist: Monikas Freunde sind im Schnitt total unbeliebt. Während sie den Beliebtheitswettbewerb gewinnt – sie hat immerhin drei Freunde – haben David, Sarah und du im Schnitt gerade mal 1,67 Freunde.
Selbst wenn wir nun ein anderes soziales Netzwerk entwerfen, kommen wir möglicherweise zum selben Ergebnis. Doch das liegt nicht daran, dass deine Beliebtheit zu wünschen übrig lässt. Stattdessen ist es so: Du bist mit beliebten Leuten befreundet, weil sie viele Freunde haben. Das ist genau derselbe Grund, warum du länger auf den Bus wartest. Es ist schlichtweg wahrscheinlicher, dass du die längere Wartezeit erwischst oder dich eben mit den Leuten bekannt machst, die viele Freunde haben und schnell neue Freundschaften schließen.
Letztendlich ist das Inspektionsparadox also kein Problem (und im engeren mathematischem Sinne auch kein Paradox). Lediglich in der statistischen Forschung muss man es mit Vorsicht genießen, da es Umfrageergebnisse verfälschen kann. Doch für dich ist das Wissen um diesen Umstand eine Möglichkeit, deine Lage aus einer anderen Perspektive zu sehen: Du bist bei beliebten Menschen sehr beliebt. Und auf den Bus wartest du nur länger, weil es andere auch tun. Das lässt einen doch direkt weniger alleine fühlen.
Quelle: Scientific American, eigene Recherche
Seit dem 24. Februar 2022 herrscht Krieg in der Ukraine. Hier kannst du den Betroffenen helfen.

